확률적(통계적) 실험 : 실험의 결과가 구체적으로 어떤 것인가는 알 수 없지만 전체 가능한 모든 결과들은 알고 있고 반복이 가능한 경우를 확률적(통계적)실험이라고 함
표본공간(sample space) : 통계적 실험의 모든 가능한 결과의 집합 S, 이산형과 연속형 표본공간으로 나눌 수 있음
사건(event) : 표본공간의 한 부분집합
확률(probability) : 통계적 실험에서 한 사건이 발행하는 가능성을 나타내기 위해 확률이란 개념을 사용하고, 이는 "아직 실현되지 않은 현상에 대하여 어떤 사건이 일어날 가능성을 0과 1 사이의 실수로 표시"하는 것
원소(element) : 어떤 실험의 결과로 나타날 수 있는 가능한 경우들, 각각의 현상을 원소라고 한다.
예)
1. 동전을 한번 던지는 실험
원소 : H(=앞면) 또는 T(=뒷면)
표본공간 : S={H,T}
2. 주사위를 한번 던지는 실험
원소 : 1,2,3,4,5,6
표본공간 S = {1,2,3,4,5,6}
사상 : 실험의 결과 짝수 눈이 나오는 경우
확률의 고전적 정의
표본공간의 모든 원소가 일어날 가능성이 같다고 가정
S = {e1, e2, e3, …., en}, 사건: A = {e1, … ei, … ek}

이산형인 경우 표본공간의 전체 원소수, 연속형인 경우 표본공간의 전체 원소에 대한 측도
확률의 상대도수적 정의
사건 A가 발생할 확률(P(A)로 표시)은 같은 조건하에서 통계적 실험을 수없이 반복 시행했을 때 사건 A가 발생하는 비율, 즉 상대도수이다.

확률의 공리적 정의
공리적확률은 표본공간S의 사건 A가 다음을 만족할 때 P(A)를 A의 확률이라 한다.
공리적 확률은 고전적 확률을 일반화시킨 확률이다. 고전적 정의에서는 모든 원소가 발생할 가능성이 같다고 가정하지만 그렇지 않을 경우가 있을 수 있으므로 확률을 포괄적으로 정리해야 한다.
표본공간 S의 사건 A의 확률 P(A)가 다음을 만족할 때 P(A)를 A의 확률이라 한다.
① 0<=P(A)<=1, P(A)는 0과 1사이에 있다.
② P(S)=1, 표본공간의 확률은 1이다.
③ A1, A2, …, Ai, …가 서로 배반사건일 때 다음이 성립된다.
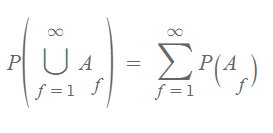
확률의 계산
순열(비복원) : 순서가 고려된 경우의 수는
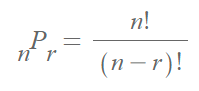
조합(비복원) : 순서가 고려되지 않은 경우의 수는
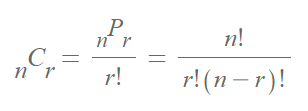
중복순열(복원) : 순서가 고려된 중복이 가능한 순열
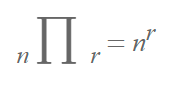
중복조합(복원) : 순서가 고려되지 않은 중복이 가능한 조합
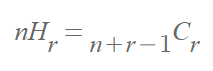
확률의 덧셈법칙
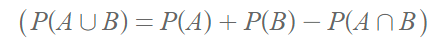
만일 A와 B의 교집합이 공집합이면 A, B를 서로 배반사건(mutually exclusive events)이라고 한다.
여사건의 확률
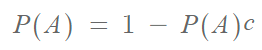
조건부 확률
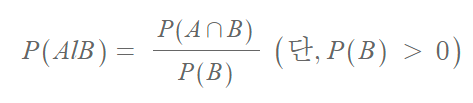
확률의 곱셈법칙
P(A) > 0, P(B) > 0이면
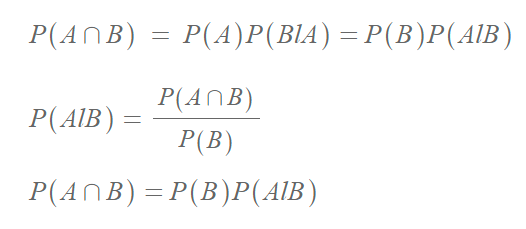
독립사건
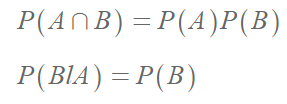
배반사건
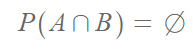
'데이터분석 > 수학' 카테고리의 다른 글
| 확률변수 (0) | 2022.05.01 |
|---|---|
| 수학에 사용되는 그리스어 (0) | 2020.08.14 |